AI & Python #25: Let's Build Your First Machine Learning Model in Python

A complete guide to build a basic ML model.

Flickr

If you’re not into coding, go to settings and turn off notifications for “AI & Python” (leave the rest the same to keep receiving my other emails)

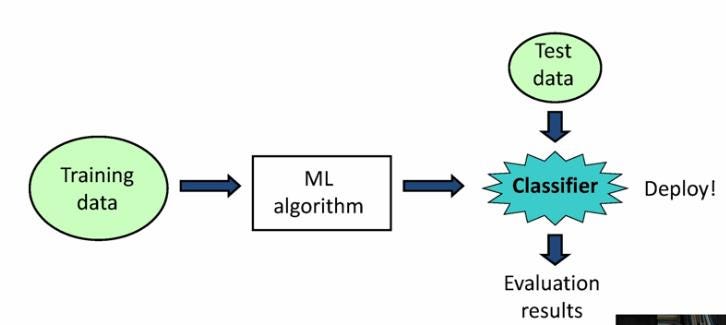
If you’re learning Python and would like to develop a machine learning model then a library that you want to seriously consider is scikit-learn. Scikit-learn (also known as sklearn) is a machine learning library used in Python that provides many unsupervised and supervised learning algorithms.

In this simple guide, we’re going to create a machine learning model that will predict whether a movie review is positive or negative. This is known as binary text classification and will help us explore the scikit-learn library while building a basic machine learning model from scratch. Below are the concepts we’re going to learn in this guide.

Table of Contents
1. The Dataset and The Problem to Solve
2. Preparing The Data
 - Reading the dataset
 - Dealing with Imbalanced Classes
 - Splitting data into train and test set
3. Text Representation (Bag of Words)
 - CountVectorizer
 - Term Frequency, Inverse Document Frequency (TF-IDF)
 - Turning our text data into numerical vectors
4. Model Selection
 - Supervised vs Unsupervised learning
 - Support Vector Machines (SVM)
 - Decision Tree
 - Naive Bayes
 - Logistic Regression
5. Model Evaluation
 - Mean Accuracy
 - F1 Score
 - Classification report
 - Confusion Matrix
6. Tuning the Model
 - GridSearchCV

The Dataset and The Problem to Solve

👉 Dataset: In this guide, we’ll use an IMDB dataset of 50k movie reviews available on Kaggle. The dataset contains 2 columns (review and sentiment) that will help us identify whether a review is positive or negative.

Problem formulation: Our goal is to find which machine learning model is best suited to predict sentiment (output) given a movie review (input).

Preparing The Data

Reading the dataset

After you download the dataset, make sure the file is in the same place where your Python script is located. Then, we’ll read the file using the Pandas library.

import pandas as pd

df_review = pd.read_csv('IMDB Dataset.csv')
df_review

Note: If you don’t have some of the libraries used in this guide, you can easily install a library with pip on your terminal or command prompt (e.g.,pip install scikit-learn)

The dataset looks like the picture below.

Image by author

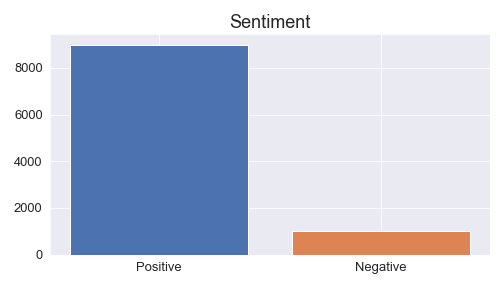
This dataset contains 50000 rows; however, to train our model faster in the following steps, we’re going to take a smaller sample of 10000 rows. This small sample will contain 9000 positive and 1000 negative reviews to make the data imbalanced (so I can teach you undersampling and oversampling techniques in the next step)

We’re going to create this small sample with the following code. The name of this imbalanced dataset will bedf_review_imb

df_positive = df_review[df_review['sentiment']=='positive'][:9000]
df_negative = df_review[df_review['sentiment']=='negative'][:1000]

df_review_imb = pd.concat([df_positive, df_negative])

Dealing with Imbalanced Classes

In most cases, you’ll have a large amount of data for one class, and much fewer observations for other classes. This is known as imbalanced data because the number of observations per class is not equally distributed.

Let’s take a look at how our df_review_imb dataset is distributed.

Image by author

As we can see there are more positive than negative reviews in df_review_imb so we have imbalanced data.

To resample our data we use the imblearn library. You can either undersample positive reviews or oversample negative reviews (you need to choose based on the data you’re working with). In this case, we’ll use the RandomUnderSampler

from imblearn.under_sampling import  RandomUnderSampler

rus = RandomUnderSampler(random_state=0)
df_review_bal, df_review_bal['sentiment']=rus.fit_resample(df_review_imb[['review']],
                                                           df_review_imb['sentiment'])
df_review_bal

First, we create a new instance of RandomUnderSampler (rus), we add random_state=0 just to control the randomization of the algorithm. Then we resample the imbalanced dataset df_review_imb by fitting rus with rus.fit_resample(x, y) where “x” contains the data which have to be sampled and “y” corresponds to labels for each sample in “x”.

After this, x and y are balanced and we’ll store it in a new dataset named df_review_bal. We can compare the imbalanced and balanced dataset with the following code.

IN [0]: print(df_review_imb.value_counts(‘sentiment’))
        print(df_review_bal.value_counts(‘sentiment’))

OUT [0]:positive    9000
        negative    1000

        negative    1000
        positive    1000

As we can see, now our dataset is equally distributed.

Note 1: If you get the following error when using the RandomUnderSampler

IndexError: only integers, slices (`:`), ellipsis (`…`), numpy.newaxis (`None`) and integer or boolean arrays are valid indices

You can use an alternative to RandomUnderSampler. Try the code below:

# option 2
length_negative = len(df_review_imb[df_review_imb['sentiment']=='negative'])
df_review_positive = df_review_imb[df_review_imb['sentiment']=='positive'].sample(n=length_negative)
df_review_non_positive = df_review_imb[~(df_review_imb['sentiment']=='positive')]

df_review_bal = pd.concat([
    df_review_positive, df_review_non_positive
])
df_review_bal.reset_index(drop=True, inplace=True)
df_review_bal['sentiment'].value_counts()

The df_review_bal dataframe should have now 1000 positive and negative reviews as shown above.

Splitting data into train and test set

Before we work with our data, we need to split it into a train and test set. The train dataset will be used to fit the model, while the test dataset will be used to provide an unbiased evaluation of a final model fit on the training dataset.

We’ll use sklearn’s train_test_split to do the job. In this case, we set 33% to the test data.

from sklearn.model_selection import train_test_split

train, test = train_test_split(df_review_bal, test_size=0.33, random_state=42)

Now we can set the independent and dependent variables within our train and test set.

train_x, train_y = train['review'], train['sentiment']
test_x, test_y = test['review'], test['sentiment']

Let’s see what each of them mean:

• train_x: Independent variables (review) that will be used to train the model. Since we specified test_size = 0.33, 67% of observations from the data will be used to fit the model.

• train_y: Dependent variables (sentiment) or target label that need to be predicted by this model.

• test_x: The remaining 33% of independent variables that will be used to make predictions to test the accuracy of the model.

• test_y: Category labels that will be used to test the accuracy between actual and predicted categories.

Text Representation (Bag of Words)